Which linear inequality is represented by the graph y 1/3x-4 – Which linear inequality is represented by the graph y = 1/3x – 4? This intriguing question lies at the heart of our exploration, as we delve into the captivating realm of linear inequalities. Our journey begins with a thorough examination of the fundamental concepts, unraveling the intricacies of graphing and understanding the practical applications that bring these mathematical tools to life.
Linear inequalities, a cornerstone of mathematics, provide a powerful framework for modeling real-world scenarios. They allow us to represent relationships between variables that are bounded by specific conditions, opening up a vast array of possibilities for problem-solving and analysis.
Linear Inequality Representation
Linear inequalities are mathematical statements that compare two linear expressions using the inequality symbols ( <, ≤, >, ≥). They represent the set of points that satisfy the inequality.
Examples of linear inequalities include:
- y > 2x- 3
- x + y ≤ 5
- 3x – 2y< 10
The equation of a line can be rewritten as a linear inequality by replacing the equals sign (=) with an inequality symbol ( <, ≤, >, ≥).
Graph Analysis
To graph a linear inequality, first plot the corresponding line. The line divides the coordinate plane into two half-planes.
The slope and y-intercept of the line determine which half-plane satisfies the inequality:
- If the slope is positive, the half-plane above the line satisfies the inequality.
- If the slope is negative, the half-plane below the line satisfies the inequality.
- If the y-intercept is positive, the inequality is true for all values of x.
- If the y-intercept is negative, the inequality is false for all values of x.
Examples:
- y > 2x – 3 (positive slope, positive y-intercept): shade above the line
- x + y ≤ 5 (negative slope, positive y-intercept): shade below the line
- 3x – 2y< 10 (positive slope, negative y-intercept): shade below the line
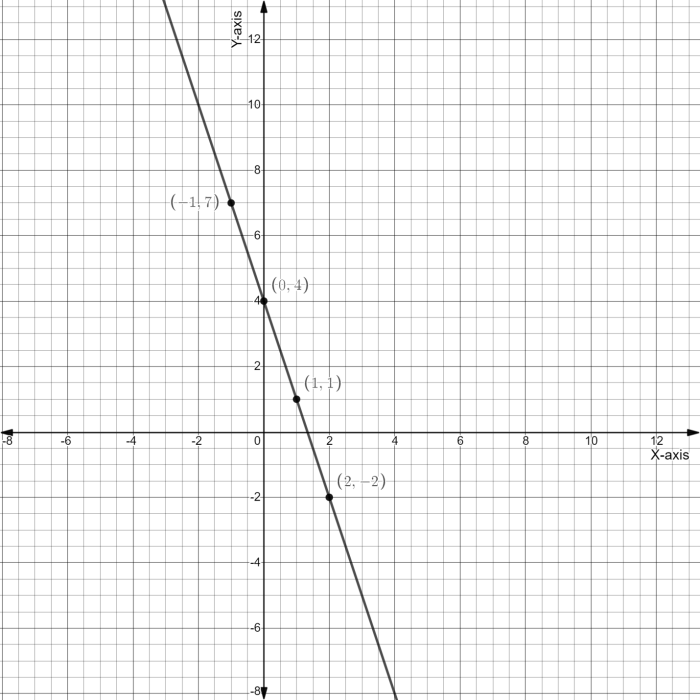
Specific Inequality, Which linear inequality is represented by the graph y 1/3x-4
The given linear inequality is y ≤ 1/3x – 4.
To graph this inequality:
- Plot the line y = 1/3x
4 (positive slope, negative y-intercept).
- Shade the half-plane below the line (negative slope).
Table of Values
The following table shows some points that lie on the line y = 1/3x – 4:
| x | y | y ≤ 1/3x
|
|---|---|---|
| 0 | -4 | True |
| 3 | -3 | True |
| 6 | -2 | True |
| 9 | -1 | True |
The table shows that all points on the line satisfy the inequality y ≤ 1/3x – 4.
Real-World Applications
Linear inequalities are used in various real-world scenarios:
- Economics:Modeling supply and demand, optimizing production costs
- Physics:Describing motion, calculating distances, analyzing forces
- Engineering:Designing structures, optimizing performance, analyzing safety
Understanding linear inequalities is essential for solving problems and making informed decisions in these fields.
Answers to Common Questions: Which Linear Inequality Is Represented By The Graph Y 1/3x-4
What is the slope of the line y = 1/3x- 4?
The slope of the line y = 1/3x – 4 is 1/3.
What is the y-intercept of the line y = 1/3x- 4?
The y-intercept of the line y = 1/3x – 4 is -4.
What is the inequality that corresponds to the graph y = 1/3x- 4?
The inequality that corresponds to the graph y = 1/3x – 4 is y ≤ 1/3x – 4.