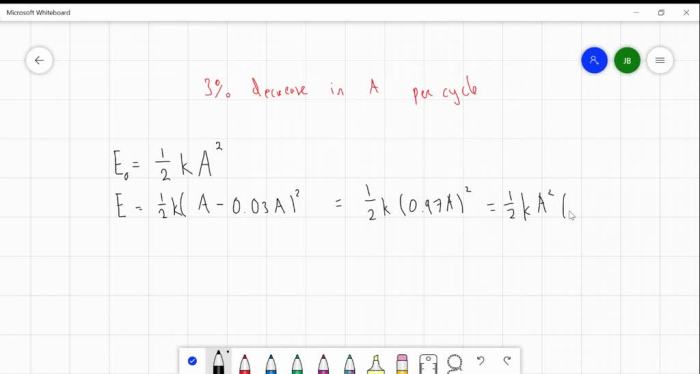The amplitude of a lightly damped oscillator decreases by – The amplitude of a lightly damped oscillator decreases exponentially over time due to the dissipation of energy through damping forces. This phenomenon is crucial in understanding the behavior of oscillating systems in various fields, from physics and engineering to biology and economics.
Damping forces, such as friction, air resistance, and internal material resistance, oppose the motion of the oscillator, causing a gradual reduction in its amplitude. The rate of decay depends on the damping coefficient, which characterizes the strength of the damping force.
Understanding the Amplitude of a Lightly Damped Oscillator

In the realm of oscillations, the amplitude represents the maximum displacement of an oscillator from its equilibrium position. In the case of a lightly damped oscillator, the amplitude gradually decreases over time due to the dissipative nature of damping forces.
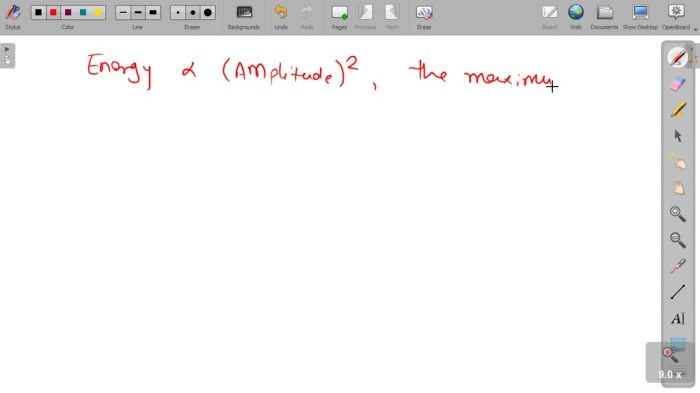
The amplitude of a lightly damped oscillator is directly proportional to the initial energy of the system. A higher initial energy results in a larger amplitude, as the oscillator possesses more potential energy to be converted into kinetic energy during its motion.
Causes of Amplitude Decrease, The amplitude of a lightly damped oscillator decreases by
Damping forces play a crucial role in reducing the amplitude of an oscillator. Damping occurs when energy is dissipated from the system through various mechanisms, such as friction, viscosity, or resistance.
There are different types of damping, each with its own effect on amplitude:
- Viscous damping:Occurs due to the resistance of a fluid medium to the motion of an object. It is proportional to the velocity of the oscillator and causes a gradual decrease in amplitude.
- Coulomb damping:Occurs due to friction between two surfaces in contact. It is independent of velocity and causes a sudden decrease in amplitude at each contact point.
External forces can also contribute to amplitude decrease. For example, if an external force is applied in the opposite direction of the oscillator’s motion, it will reduce the amplitude by absorbing energy from the system.
Mathematical Analysis of Amplitude Decay
The motion of a damped oscillator is governed by the following differential equation:
mx” + bx’ + kx = 0
where:
- m is the mass of the oscillator
- b is the damping coefficient
- k is the spring constant
- x is the displacement from equilibrium
Solving this differential equation yields the expression for the amplitude as a function of time:
A(t) = A0e -bt/2m
where A 0is the initial amplitude.
This equation shows that the amplitude decays exponentially with time, with the rate of decay determined by the damping coefficient b.
Applications of Amplitude Decay
Amplitude decay is a ubiquitous phenomenon in real-world systems, including:
- Pendulums
- Spring-mass systems
- Electrical circuits
Understanding amplitude decay is crucial in various fields, such as:
- Engineering:To design systems with optimal damping to control oscillations
- Physics:To study the behavior of oscillating systems and energy dissipation
- Biology:To analyze the dynamics of biological systems, such as heartbeats and muscle contractions
FAQ Explained: The Amplitude Of A Lightly Damped Oscillator Decreases By
What is the cause of amplitude decrease in a lightly damped oscillator?
Damping forces, such as friction and air resistance, oppose the motion of the oscillator, causing a gradual reduction in its amplitude.
How does the damping coefficient affect the rate of amplitude decay?
The damping coefficient is a measure of the strength of the damping force. A higher damping coefficient leads to a faster rate of amplitude decay.
What are some real-world examples of amplitude decay due to damping?
Examples include the swinging of a pendulum, the vibration of a guitar string, and the decay of sound waves in a room.