Ch 7 notes right triangles answer key – Embark on a captivating journey into the world of right triangles with our comprehensive guide and ch 7 notes answer key. Delve into the fundamental concepts, explore practical applications, and master the art of solving right triangle problems with ease.

From understanding the Pythagorean theorem to harnessing the power of trigonometric ratios, this guide empowers you with the knowledge and skills to conquer any right triangle challenge that comes your way.

Understanding Right Triangles

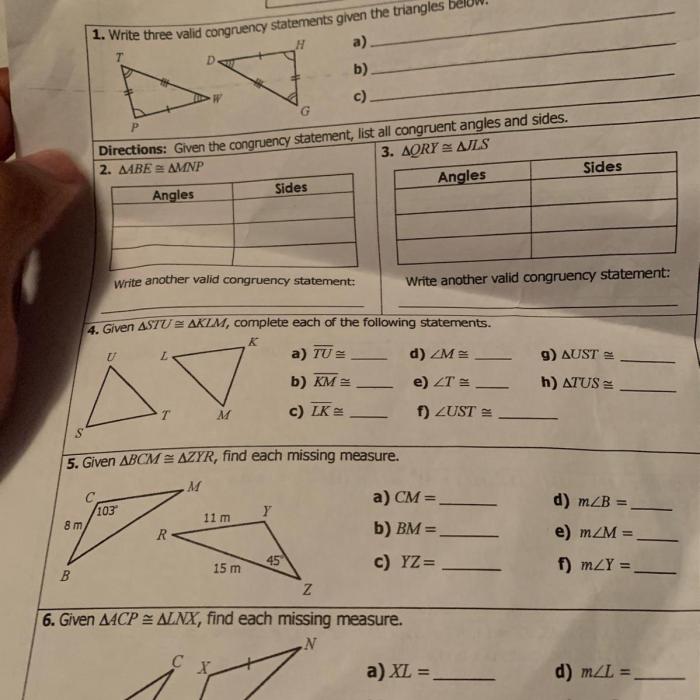
Right triangles are fundamental geometric shapes with one angle measuring 90 degrees. They possess unique properties and relationships that have significant applications in various fields.

Properties of Right Triangles

Key properties of right triangles include:

• The sum of the interior angles is always 180 degrees.
• The square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (Pythagorean theorem).
• The ratio of the sides opposite and adjacent to an angle is equal to the tangent of that angle.

Applications of Right Triangles

Right triangles find widespread use in real-world applications, such as:

• Architecture and construction:Calculating roof angles, determining beam lengths, and designing staircases.
• Navigation:Determining distances and angles using trigonometry.
• Engineering:Designing bridges, analyzing forces, and calculating stresses.

Pythagorean Theorem

The Pythagorean theorem is a fundamental relation in right triangles that states:

a²+ b ²= c ²

where aand bare the lengths of the two shorter sides (legs) and cis the length of the hypotenuse.

This theorem is crucial for solving right triangle problems and has numerous applications in various fields.

Solving Right Triangle Problems

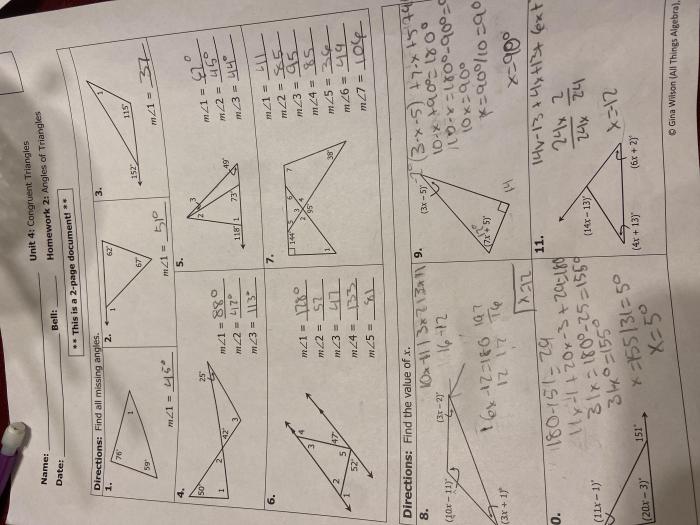
Solving right triangle problems involves applying trigonometric ratios and the Pythagorean theorem to find unknown sides and angles. Here’s a step-by-step approach:1.

• -*Identify the given information

  Determine which sides and angles are known and which are unknown.

• 2.

-*Use trigonometric ratios

If you have an angle and the length of one side, you can use the trigonometric ratios (sine, cosine, and tangent) to find the lengths of the other sides.

• 3.

-*Apply the Pythagorean theorem

If you have the lengths of two sides, you can use the Pythagorean theorem (a^2 + b^2 = c^2) to find the length of the third side.

• 4.

-*Solve for the unknown

Use algebraic equations to solve for the unknown sides or angles.

Practice Problems

Problem 1: A right triangle has a hypotenuse of 10 cm and an angle of 30 degrees. Find the lengths of the other two sides.Solution:Let the length of the side opposite the 30-degree angle be x cm.

Using sine ratio

sin(30) = x/10

• Solving for x

  x = 10

• sin(30) = 5 cm
• The length of the other side (adjacent to the 30-degree angle) is 10
• 5 = 5 cm.

Problem 2: A ladder leans against a wall, forming a right triangle. The ladder is 10 feet long and the base of the ladder is 6 feet from the wall. Find the height of the ladder.Solution:Let the height of the ladder be h feet.

Using Pythagorean theorem

h^2 + 6^2 = 10^2

• Solving for h

  h = √(10^2

• 6^2) = 8 feet

Using Trigonometric Ratios

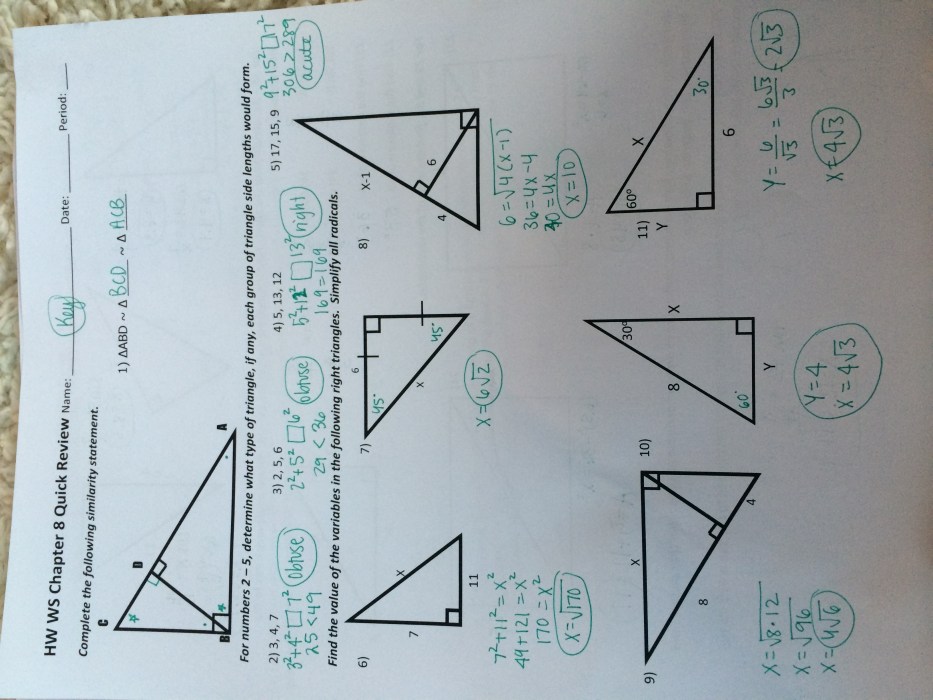
Trigonometric ratios are ratios of the lengths of the sides of a right triangle. They are used to solve right triangle problems and have many applications in real-world scenarios, such as surveying, navigation, and architecture.

Sine, Cosine, and Tangent

The three main trigonometric ratios are sine, cosine, and tangent. They are defined as follows:

• Sine (sin) = opposite side / hypotenuse
• Cosine (cos) = adjacent side / hypotenuse
• Tangent (tan) = opposite side / adjacent side

These ratios can be used to find the length of any side of a right triangle if the lengths of the other two sides are known.

Applications of Trigonometric Ratios

Trigonometric ratios have many applications in real-world scenarios, including:

• Surveying: Trigonometric ratios are used to measure the height of buildings and other objects.
• Navigation: Trigonometric ratios are used to calculate the distance between two points on a map.
• Architecture: Trigonometric ratios are used to design buildings and other structures.

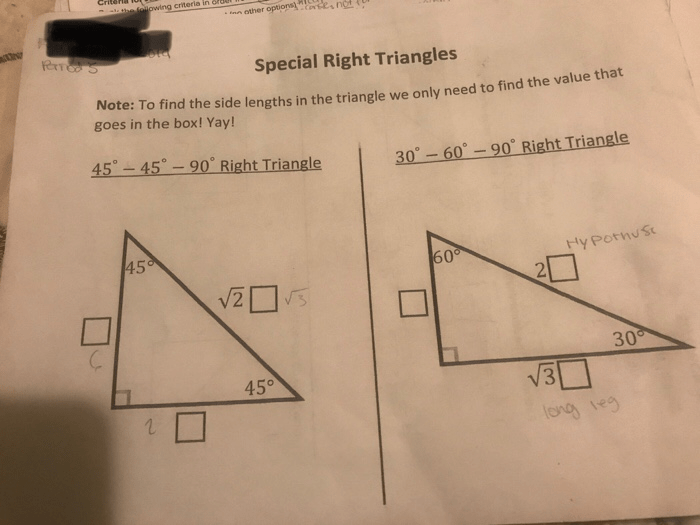
Special Right Triangles

Special right triangles are triangles with specific angle measures that lead to predictable side length ratios. These triangles occur frequently in various applications and provide convenient shortcuts for solving problems involving right triangles.

30-60-90 Triangles

30-60-90 triangles have angles of 30°, 60°, and 90°. The side opposite the 30° angle is half the length of the hypotenuse, and the side opposite the 60° angle is √3 times half the length of the hypotenuse.

Applications:

• Finding heights of objects using shadows
• Determining distances using trigonometry
• Solving geometric problems involving equilateral triangles

45-45-90 Triangles

45-45-90 triangles have angles of 45°, 45°, and 90°. The two legs of the triangle are equal in length, and the hypotenuse is √2 times the length of a leg.

Applications:

• Finding diagonals of squares and rectangles
• Solving problems involving inscribed circles
• Determining distances using the Pythagorean theorem

Using Special Right Triangles, Ch 7 notes right triangles answer key

To use special right triangles to simplify calculations:

• Identify the type of special right triangle based on its angle measures.
• Apply the appropriate side length ratios to determine unknown side lengths.
• Use trigonometric ratios to find angles or other measurements.

Examples

1. 30-60-90 Triangle:If the hypotenuse of a 30-60-90 triangle is 10 cm, the side opposite the 30° angle is 5 cm, and the side opposite the 60° angle is 5√3 cm.
2. 45-45-90 Triangle:If a square has a side length of 5 cm, its diagonal is 5√2 cm.

Applying Right Triangle Concepts

Right triangle concepts find widespread applications in various fields, including architecture, engineering, and surveying. Understanding right triangles is crucial for solving practical problems and making accurate measurements in these disciplines.

Architecture

In architecture, right triangles are used to determine the height of buildings, calculate roof angles, and design aesthetically pleasing structures. For instance, the Pythagorean theorem is employed to calculate the height of a building based on its base and shadow length.

Engineering

In engineering, right triangles are essential for analyzing forces, calculating stresses, and designing bridges, buildings, and other structures. For example, engineers use trigonometric ratios to determine the forces acting on a bridge truss or to calculate the angle of a support beam.

Surveying

In surveying, right triangles are used to measure distances, determine elevations, and create maps. Surveyors use theodolites and other instruments to measure angles and distances, which are then used to calculate the coordinates of points and create accurate maps.

Query Resolution: Ch 7 Notes Right Triangles Answer Key

What is the Pythagorean theorem?

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

How do I use trigonometric ratios to solve right triangle problems?

Trigonometric ratios (sine, cosine, and tangent) relate the lengths of the sides of a right triangle to the angles. By using these ratios, you can find unknown side lengths or angles in right triangle problems.

What are some real-world applications of right triangles?

Right triangles have numerous applications in fields such as architecture, engineering, surveying, and navigation. They are used to calculate heights, distances, and angles in various practical settings.